Ціль: зрозуміти бінарну систему числення, шістнадцяткове представлення і представлення знакових і беззнакових чисел.
Для вирішення задач з використанням комп'ютерних систем нам потрібно розуміти числа і що вони означають. Кожна цифра в десятковій системі числення має позицію (розряд) і значення (цінність). Позиція - це степінь числа 10, а цінність - значення з множини { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Таким чином, десяткове число - це просто комбінація цифр, чисельно рівна сумі всіх цифр помножених на 10 в степені позиції цифри (позиції рахуються справа, починаючи від нуля). Наприклад
9463 = 9000 + 400 + 60 + 3
= 9•1000 + 4•100 + 6•10 + 3•1
= 9•103 + 4•102 + 6•101 + 3•100
Дробові числа можна представити з використанням від'ємних степенів від десяти. Наприклад,
92.34 = 90 + 2 + 0.3 + 0.04
= 9•10 + 2•1 + 3•0.1 + 4•0.01
= 9•101 + 2•100 + 3•10-1 + 4•10-2

Подібним чином, кожна цифра в бінарному (двійковому) числі має позицію і цінність. В двійкових числах позиція - це степінь від двох, а цінність - цифра з множини { 0, 1 }. Тож, двійкове число - це просто комбінація цифр, чисельно рівна сумі всіх цифр помножених на 2 в степені позиції цієї цифри (позиції рахуються справа і від нуля). Щоб уникнути плутанини між десятковими та двійковими числами, ми будемо ставити нижній індекс 2 після числа, що означає двійкову систему. Через те, як працюють цифрові системи, більшість двійкових чисел у цій статті матимуть 8, 16 або 32 біти (один біт означає одну цифру в двійковому числі, 0 або 1). 8-бітове число називається байтом, а 16-бітове число — півсловом. Наприклад, 8-бітове двійкове число для 174 таке
1010 11102 =
= 1•27 + 0•26 + 1•25 + 0•24 + 1•23 + 1•22 + 1•21 + 0•20
= 1•128 + 0•64 + 1•32 + 0•16 + 1•8 + 1•4 + 1•2 + 0•1
= 128 + 0 + 32 + 0 + 8 + 4 + 2 + 0 = 174
Під час роботи з бінарними числами на комп'ютері буде зручно запам'ятати деякі степені числа 2, як показано в таблиці 1.
|
Степінь двійки |
Десяткове значення |
|
20 |
1 |
|
21 |
2 |
|
22 |
4 |
|
23 |
8 |
|
24 |
16 |
|
25 |
32 |
|
26 |
64 |
|
27 |
128 |
|
28 |
256 |
|
29 |
512 |
|
210 |
1024 |
|
211 |
2048 |
|
212 |
4096 |
|
213 |
8192 |
|
214 |
16384 |
|
215 |
32768 |
|
216 |
65536 |
|
220 |
біля мільйону |
|
230 |
біля мільярду |
Шістнадцяткові числа
Бінарні числа - це "природна мова" для комп'ютерів, але велика неприємність для нас людей. Довгі одноманітні набори одиниць та нулів дуже важко сприймати. Щоб спростити роботу з двійковими числами, люди використовують споріднену систему числення, яка називається шістнадцятковою, яка використовує основу 16. Так само, як у десятковій та двійковій системах числення, кожна шістнадцяткова цифра має розряд та значення. В цьому випадку позиція - це степінь від 16, а значення - цифра з множини { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F }. Як бачите, шістнадцяткові числа мають більше варіантів для значень, ніж у десятковому форматі; тому ми додаємо літери від A до F, як показано в Таблиці 2. Шістнадцяткове число — це комбінація його цифр, помножених на степені числа 16. Щоб уникнути плутанини між різними форматами, ми ставимо 0x перед числом, що означає шістнадцяткове число. Шістнадцяткове представлення — це зручний механізм для нас, людей, для визначення двійкової інформації, оскільки людям просто конвертувати між собою двійкові та шістнадцяткові числа. Шістнадцяткову систему числення часто скорочують як «hex». Півбайт(nibble) визначається як 4 біти або одна шістнадцяткова цифра. Кожне значення 4-бітного півбайта відображається в унікальну шістнадцяткову цифру, як показано в Таблиці 2.
| Hex-цифра | Десяткове значення | Бінарне значення |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Тепер, зіставляючи по таблиці бінарні півбайти з hex-цифрами можна записати будь-яке бінарне число у шістнадцятковому вигляді. Наприклад, hex-число для 16-бітного бінарного 1001 1010 0111 1101 буде 0x9A7D, яке в свою чергу конвертується в десяткове число так:
0x9A7D = 9•163 + 10•162 + 7•161 + 13•160
= 9•4096 + 10•256 + 7•16 + 13•1
= 36864 + 2560 + 112 + 13 = 39549
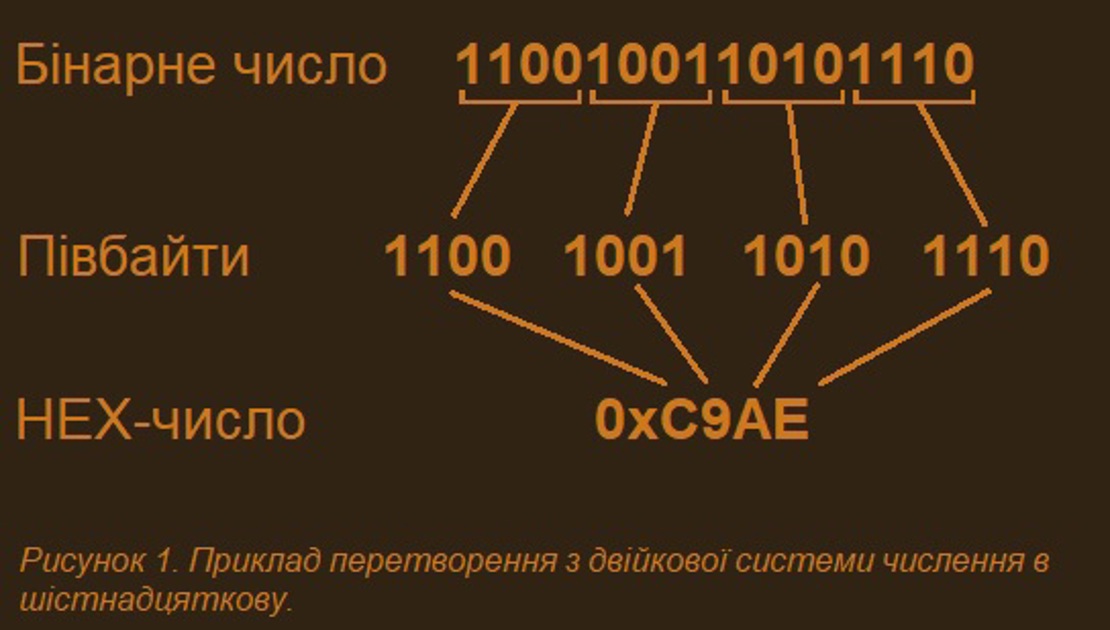
На рисунку 1 проілюстровано спосіб перетворення з двійкової системи числення в шістнадцяткову в два кроки:
- Розділити двійкове число на півбайти(нібли);
- Перетворити кожен півбайт у відповідну йому шістнадцяткову цифру.
За тим самим принципом можна перетворювати числа з шістнадцяткової системи назад в бінарну.
Примітка. Різні середовища комп'ютерного програмування можуть використовувати різні варіанти символьних позначень для позначення чисел у шістнадцятковому форматі. Наприклад, двійкове число 01111010. Деякі мови асемблера використовують $7A. Деякі мови асемблера використовують 7AH. Мова C використовує 0x7A. Симулятор LC-3 Патта використовує x7A.
Формати чисел
Кількість бітів визначає точність і діапазон можливих значень. Наприклад, 8-бітний (1 байт) числовий формат може представляти 256 різних чисел. 8-бітний цифро-аналоговий перетворювач (ЦАП) може генерувати 256 різних аналогових виходів. 8-бітний аналого-цифровий перетворювач (АЦП) може вимірювати 256 різних аналогових вхідних рівнів сигналу. У таблиці 3 показано зв'язок між точністю в двійкових розрядах та діапазоном можливих значень.
| Кількість біт | Кількість байт | Діапазон значень |
| 4 | 0.5 | 0-15 |
| 8 | 1 | 0-255 |
| 16 | 2 | 0-65535 |
| 32 | 4 | 0-4294967296 |
| n | n/8 | 2n |
Байт містить 8 бітів, як показано на рисунку 2, де кожен біт b7,...,b0 є двійковим і має значення 1 або 0. Ми визначаємо b7 як старший біт, а b0 як молодший біт.
![]()
Рисунок 2. 8-бітний формат
Числа можуть бути знаковими або беззнаковими. Знакові числа це такі числа які можуть бути додатними або від'ємними (мають знак). Беззнакові числа, відповідно не мають знака, тож будуть завжди додатними. Якщо байт використовується для представлення беззнакового числа, то значення цього числа рахується так:
N = 128•b7 + 64•b6 + 32•b5 + 16•b4 + 8•b3 + 4•b2 + 2•b1 + b0
а отже абсолютно так само як ми робили при перетворенні бінарного числа на десяткове.
Беззнакові числа можуть зберігати лише невід’ємні значення — від 0 до максимально можливого для заданої кількості бітів. Але в багатьох задачах необхідно оперувати також і від’ємними числами. Для цього у цифрових системах використовуються спеціальні способи кодування — подання знакових чисел. Як це зробити? Здається все просто: відвести перший (старший) біт для знаку (0 — додатне, 1 — від’ємне), а решту бітів — для величини числа. Такий метод називається “знак-величина” (sign-magnitude). Наприклад, для 8-бітного формату: 000010102 = +10, 100010102 = -10. Недолік цього підходу в тому, що з’являється дві форми нуля: 000000002 (+0) і 100000002 (–0). Крім того, арифметичні операції з такими числами ускладнюються. Тому сучасні цифрові системи застосовують інший метод.
Система числення з доповненням до двох є найпоширенішим підходом, який використовується для визначення від'ємних чисел у двійковій системі числення. Щоб отримати від'ємне число, потрібно інвертувати всі цифри додатного числа (обернений код) і додати одиницю до результату. Наприклад, для числа 20 у двійковій системі з 8 біт, спочатку отримуємо двійкове представлення 000101002, потім інвертуємо його до 111010112, і нарешті додаємо 1, щоб отримати 111011002 (-20).
Якщо байт використовується для представлення від'ємного числа, то значення цього числа розраховується так
N = -128•b7 + 64•b6 + 32•b5 + 16•b4 + 8•b3 + 4•b2 + 2•b1 + b0
8-бітним (1-байтовим) числом можна записати 256 різних знакових значень. Найменше знакове 8-бітове число -128, а найбільше 127. Наприклад, 100000102 = -128 + 2 = -126. Інші приклади наведено в таблиці 4.
|
Бінарні |
Hex |
Розрахунок |
Десяткові |
|
000000002 |
0x00 |
|
0 |
|
000100102 |
0x12 |
16+2 |
18 |
|
001001102 |
0x26 |
32+4+2 |
38 |
|
110001112 |
0xC7 |
-128+64+4+2+1 |
-57 |
|
111111112 |
0xFF |
-128+64+32+16+8+4+2+1 |
-1 |
Зверніть увагу, що той самий двійковий шаблон 111111112 може представляти як 255, так і –1. Розробнику програмного забезпечення дуже важливо стежити за форматом числа. Комп'ютер не може визначити, чи є 8-бітове число зі знаком, чи без знака. Саме програміст визначає, чи є число зі знаком, чи без знака, за допомогою конкретних інструкцій програмного коду, який він обирає для обробки цього числа. Деякі операції, такі як додавання, віднімання та зсув ліворуч (множення на 2), використовують одне й ті самі інструкції процесора як для беззнакових, так і для знакових операцій. З іншого боку, ділення та зсув праворуч (ділення на 2) вимагають різних інструкцій для беззнакових та знакових операцій.
Окрім 8-бітових чисел в цифрових системах використовують 16-бітові (2-байтові) числа, де кожен біт b15,...,b0 також є бінарним і може мати значення 0 або 1. 16-бітове число також називають півслово(halfword).
Якщо для представлення беззнакового числа використовується півслово, то значення числа рахується так
N = 32768•b15 + 16384•b14 + 8192•b13 + 4096•b12
+ 2048•b11 + 1024•b10 + 512•b9 + 256•b8 + 128•b7
+ 64•b6 + 32•b5 + 16•b4 + 8•b3 + 4•b2 + 2•b1 + b0
16-бітне беззнакове число може визначати 65536 додатних значень. Найменше беззнакове 16-бітне число дорівнює 0, а найбільше — 65535. Наприклад, 00100001100001002 або 0x2184 це 8192+256+128+4 = 8580.
Також можна представити 65536 різних значень 16-бітним знаковим числом. Найменше 16-бітне число зі знаком –32768, а найбільше 32767. Наприклад, 11010000000001002 або 0xD004 — це –32768 + 16384 + 4096 + 4 = –12284.
Коли ж півслово використовується для представлення числа у доповненні до двох зі знаком, то значення цього числа рахується так
N = -32768•b15 + 16384•b14 + 8192•b13 + 4096•b12
+ 2048•b11 + 1024•b10 + 512•b9 + 256•b8 + 128•b7
+ 64•b6 + 32•b5 + 16•b4 + 8•b3 + 4•b2 + 2•b1 + b0
Типова помилка: можна легко помилитися якщо виконувати арифметичні дії над числами різної точності. Наприклад, не можна додавати 8-бітне знакове 100111012 (-99) до 16-бітного 00100000000000002. Потрібно спочатку перетворити 8-бітне на 16-бітне і лише потім проводити операції. Перетворення робиться просто - старші пусті байти заповнюються нулями для додатного числа і одиницями для від'ємного. Наприклад 8-бітне 100111012 (-99) перетворюється на 11111111100111012
Подібним чином все вищесказане стосується і чисел більшої розрядності. Слово - 32-бітне число, подвійне слово - 64-бітне число.
У бінарній системі можна подати не лише цілі, а й дробові значення. Для цього використовують числа з фіксованою точкою. Ідея дуже проста: у всіх чисел одного формату крапка завжди стоїть в одній і тій самій позиції. По суті це звичайна послідовність бітів, ми лише домовляємося, що певна кількість розрядів зліва — це ціла частина, а решта справа — дробова. Наприклад, у 8-бітному числі можна вважати, що п'ять бітів зліва описують цілу частину, а три справа — дробову. Тоді число «виглядає» так:
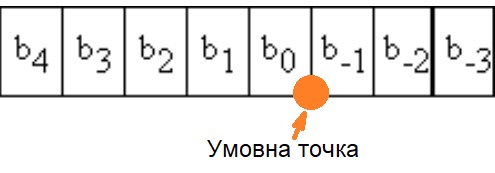
де ліві біти — цілі, а праві — дробові.
Завдяки цьому будь-який набір бітів можна тлумачити як число з наперед відомою точністю. Чим більше бітів відведено під дробову частину, тим дрібніші значення можна розрізнити, але тим менший діапазон цілих чисел. Якщо ж більше бітів залишити для цілої частини, то діапазон зростає, але дробова точність зменшується.
Значення з фіксованою точкою в цьому випадку рахується так:
001011102 = 0•24 + 0•23 + 1•22 + 0•21 + 1•20 + 1•2-1 + 1•2-2 + 0•2-3
= 4 + 1 + 0.5 + 0.25 = 5.75
